La ecuación de Mandelbrot y el conjunto de Mandelbrot se consideran uno de los fractales más bellos y fascinantes en matemáticas, y muchas personas los describen como «hermosos» debido a sus complejas y repetitivas estructuras que revelan patrones infinitos.

Alvaro Abril, Coordinador Comunicaciones Unisabaneta
Sin embargo, la frase «la ecuación más bella del universo» suele estar reservada para otra ecuación muy famosa en matemáticas y física: la fórmula de Euler.
La fórmula de Euler es:
𝑒𝑖𝜋+1=0
Esta ecuación se considera muy hermosa por varios motivos:
- Conecta cinco de los números más importantes en matemáticas: 𝑒 (la base del logaritmo natural), 𝑖 (la unidad imaginaria), 𝜋 (la relación entre la circunferencia y el diámetro de un círculo), 1 (la identidad multiplicativa) y 0 (la identidad aditiva).
- Es sorprendentemente simple y elegante, a la vez que profunda en su significado.
Por lo tanto, aunque el conjunto de Mandelbrot es altamente valorado por su belleza visual y matemática, la frase «la ecuación más bella del universo» suele referirse a la fórmula de Euler.
En palabras sencillas qué significa
En palabras sencillas, la ecuación de Mandelbrot describe un conjunto de números complejos que generan un patrón fractal, conocido como el conjunto de Mandelbrot. Este patrón es una imagen muy famosa que parece un objeto con formas repetitivas y detalles infinitos, independientemente de cuánto te acerques.

La idea básica es que tomas un número complejo 𝑐 y lo usas en una fórmula iterativa:
𝑧𝑛+1=𝑧𝑛2+𝑐
Comenzando con 𝑧0=0, calculas una serie de valores 𝑧1,𝑧2,𝑧3,…. Si estos valores permanecen limitados (no se van al infinito), entonces el número complejo 𝑐 es parte del conjunto de Mandelbrot. Si los valores se vuelven infinitamente grandes, entonces 𝑐 no está en el conjunto.
El conjunto de Mandelbrot tiene una forma característica que es muy compleja y hermosa, y se utiliza para estudiar y visualizar las propiedades de los fractales. Estos fractales tienen la peculiaridad de mostrar patrones similares en diferentes escalas, es decir, si haces zoom en una parte del fractal, seguirás viendo estructuras similares a las que ves a mayor escala.
Ejemplo práctico
Uno de los descubrimientos más sorprendentes en el ámbito de las matemáticas es que la simple ecuación Z n+1 = Z n 2 + C no sólo crea el infinitamente complejo Conjunto de Mandelbrot, sino que también podemos encontrar la misma forma icónica en los patrones creados. por muchas otras ecuaciones. De hecho, el fenómeno de la universalidad de Mandelbrot significa que cada vez que iteramos una función que en alguna parte, en alguna escala, se parece a la función parabólica Z 2 , encontraremos pequeñas copias del conjunto de Mandelbrot en el mapa de esa función.
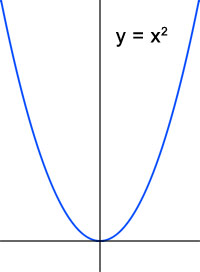
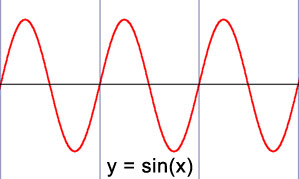
Veamos cómo se ve esto. Cuando trazamos la función básica que genera el conjunto de Mandelbrot, Z 2 , encontramos la parábola, que se muestra a continuación, a la izquierda. Ahora veamos una función diferente, la onda sinusoidal, que se representa abajo a la derecha. Estas dos funciones son muy diferentes y, sin embargo, comparten suficiente forma en común que al iterar la función seno en el plano complejo y mapear los destinos de los valores iniciales se crea una imagen fractal… ¡que contiene pequeñas réplicas del Conjunto de Mandelbrot! ÁRBITRO
 |
 |
¡Veamos algunos ejemplos! A continuación puedes ver el fractal generado al iterar la ecuación:

A la izquierda está la vista grande de la imagen fractal, y a la derecha hay una vista ampliada en detalle, que muestra una de las infinitas réplicas de Mandelbrot en este fractal.

Fractal generado con una función sinusoidal, que muestra una réplica del Conjunto de Mandelbrot.
Veamos otro ejemplo. El siguiente fractal se ha denominado fractal ‘Nova’ y se genera iterando la ecuación:
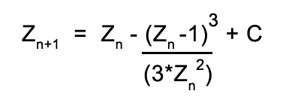
A la izquierda está la vista grande del fractal Nova y a la derecha hay un detalle ampliado que muestra una réplica perfecta de Mandelbrot.
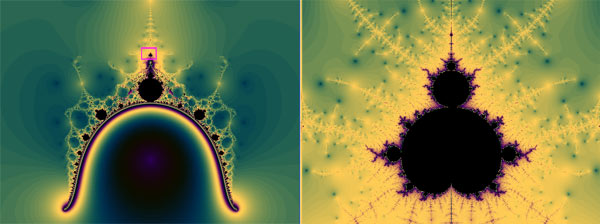
El fractal Nova, descubierto por el explorador de fractales Paul Derbyshire.
Finalmente, examinemos el fractal «Imán», que es particularmente interesante porque proviene de una ecuación física que describe la forma en que los metales como el hierro pueden ganar o perder su magnetismo. La ecuación es:
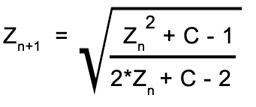
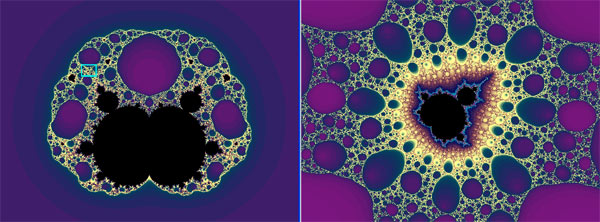
«Imán» Fractal generado con una función que describe el fenómeno conocido como percolación magnética.
Como si el Conjunto Mandelbrot en sí no fuera un campo de juego lo suficientemente infinito para explorar, ahora tenemos miles de otras fórmulas con las que jugar que generan una deslumbrante variedad de formas fractales.

